Siguiendo con la evaluación de YNC, toca ahora con la caracterización geomecánica. De acuerdo a lo indicado por Cook J. (2007), la geomecánica es el estudio de cómo se deforman los suelos y las rocas, hasta terminar a veces en su falla, en respuesta a los cambios de esfuerzos, presión, temperatura y otros parámetros ambientales(1). La geomecánica es aplicable en los aspectos de extracción de hidrocarburos, desde la exploración hasta la producción, así como el abandono de los pozos, y a través de todas las escalas presentes en los pozos, pasando por las operaciones de disparos y perforación, hasta una escala tan grande como la del modelado de cuencas y yacimientos petroleros(2).
La
finalidad de los modelos es relacionar la información disponible con las
propiedades mecánicas de la roca, esfuerzos y presión de poro presentes
requeridas cuando no es posible obtener muestras o núcleos. Un modelo
geomecánico bien construido permite determinar el estado de esfuerzos en el
yacimiento, sus propiedades mecánicas y térmicas en la formación de interés o
en estratos aledaños en cualquier dirección del campo analizado.
Los
componentes de un modelo geomecánico son: el modelo del campo de esfuerzos
actuando en el área incluida la dirección y magnitud de los tres (3) esfuerzos
principales, las propiedades mecánicas de la roca, la presión de poro y las
propiedades térmicas de la roca. Estos parámetros son utilizados para muchos
análisis posteriores como, por ejemplo: diseñar estrategias de control de
arena, diseño de modelos numéricos para simular yacimientos sensibles a esfuerzos,
optimización los procesos de perforación, predicción de la estabilidad del
pozo, entre otros.
En
la Figura 1 se ven representados los pasos a seguir mediante la elaboración de
un modelo geomecánico y que sirva para la generación de un modelo robusto en
donde se puedan identificar los intervalos o Sweet Spots que más adelante
abordaremos.
Fuente: Sánchez Carlos (2013).
Figura 1: Pasos a seguir para la
elaboración de un modelo geomecánico.
Para
establecer este modelo propuesto por Sánchez (2013), vamos a hacer mención de
aquellos parámetros que hay que considerar en el recuadro enmarcado en rojo de
la figura 1, entre ellos, el campo de esfuerzos, Módulo de Young y Relación de
Poisson:
Campo de
Esfuerzos
El
campo de esfuerzos de cualquier punto de la corteza terrestre está definido por
cuatro elementos: los tres esfuerzos ortogonales principales y la presión de
poros (Almeida et al., 2010). En la Figura 2, se presenta un esquema que
muestra los diferentes tipos de fuerzas actuantes en una superficie de una
muestra en estudio.
Todas las rocas que componen la corteza terrestre están sometidas a tres esfuerzos ortogonales principales: un esfuerzo vertical de sobrecarga (σv), originado por los estratos que se encuentran suprayacentes, un esfuerzo horizontal máximo (σHmax) y un esfuerzo horizontal mínimo (σhmin). Estas tres componentes más la presión de poros conforman el tensor de esfuerzos en cualquier punto de la corteza terrestre (esfuerzos efectivos).
Fuente: Guacuto, 2017.
Figura 2: Representación de los
esfuerzos ortogonales principales.
Propiedades Mecánicas de la Roca
De
acuerdo a lo establecido por Cook J. (2007), son características únicas de la
roca, de tipo cuantitativo, que permiten predecir el comportamiento mecánico de
formaciones rocosas, estas pueden ser utilizadas en el planteamiento de modelos
analíticos y numéricos de predicción, estas propiedades mecánicas son el
resultado de su composición mineralógica, estructura e historia geológica,
deformación e impacto ambiental, incluyendo los procesos de alteración y
meteorización, dichas propiedades que vamos a mencionar de acuerdo al enfoque
de esta lectura son:
Módulo de Young
Como
señala Gutiérrez et al., (1970), es una medida de la rigidez de la roca al
aplicarle una carga unidimensional. Este representa la deformación axial del
material en función de la carga aplicada, se puede medir en el laboratorio
(conocidas como medidas estáticas) usando núcleos o calcular de registros (medidas
dinámicas, derivadas de estos), existen numerosas correlaciones para su
estimación.
Para
un material elástico lineal e isótropo, el módulo de Young tiene el mismo valor
para una tracción que para una compresión, siendo una constante independiente
del esfuerzo siempre que no exceda de un valor máximo denominado límite
elástico, y es siempre mayor que cero. Tanto el módulo de
Young como el límite elástico son distintos para los diversos materiales. El
módulo de elasticidad es una constante elástica que, al igual que el límite
elástico, puede encontrarse empíricamente con base al ensayo de tracción del
material (Figura 3).
Figura 3: Representación
de la estimación de Young.
Para
un material isotrópico y elástico puede ser calculado de acuerdo a la Ecuación 1.
E=σ/є Ecuación 1
Donde:
E:
Es el módulo de elasticidad.
σ:
Es la carga ejercida sobre el área de sección transversal del objeto.
Є:
Es la deformación unitaria en cualquier punto de la muestra.
Relación de Poisson
Relaciona
la expansión de la roca lateralmente con la expansión vertical a gran
profundidad, los esfuerzos horizontales suelen ser altos, ya que gracias a que
la roca no puede deformarse a grandes profundidades, debido a rocas
suprayacentes. Esta deformación se transforma en esfuerzo que se acumula en la
roca. La Ecuación 2, describe la relación de Poisson (Faría, 2000).
v=-∈l/∈a Ecuación 2
Donde:
εl:
deformación por expansión lateral.
εa:
deformación por compresión longitudinal.
Ecuación 3
Donde:
Vp:
Velocidad de las ondas de compresión.
Vs:
Velocidad de cizallamiento.
Otro
parámetro o también llamado relación o índice, es el que corresponde a la
fragilidad en el cual nos enfocaremos ya que permite junto a los ya estudiados
parámetros geoquímicos y mencionados en el Blog anterior, definir las zonas
donde realizar el fracturamiento en YNC tipo Shale Gas.
Donde:
Vp:
Velocidad de las ondas de compresión.
Vs:
Velocidad de cizallamiento.
Otro
parámetro o también llamado relación o índice, es el que corresponde a la
fragilidad en el cual nos enfocaremos ya que permite junto a los ya estudiados
parámetros geoquímicos y mencionados en el Blog anterior, definir las zonas
donde realizar el fracturamiento en YNC tipo Shale Gas.
Índice de Fragilidad (2)
La fragilidad (capacidad de la roca a fracturarse),
es una de las propiedades mecánicas más importantes de las rocas. Sin embargo,
no existe un acuerdo en cuanto a la definición o a la forma de medirla. En el
trabajo de Vilas et al., (2011) se mencionan las diferentes formas en que
varios investigadores expresan y utilizan este concepto. Morley (1944), y
Hetényi (1966), definen la fragilidad como una falta de ductilidad. Ramsay
(1967), define la fragilidad en cuanto a la ruptura de la cohesión interna. A
continuación, se presenta el análisis realizado para determinar el índice de
fragilidad en el campo La Concepción (Gutiérrez, 2015).
El índice de fragilidad relacionado a la mineralogía
de las lutitas está regido por la Ecuación 4, el cual fue calculado en función
del porcentaje de COT estimado por los autores anteriormente mencionados.
Ecuación 4
Si se tiene información sobre los valores de %COT en peso, la
Ecuación 5 es aplicada para anexar este parámetro al cálculo y así, obtener
resultados más precisos.
Ecuación 5
Donde:
IF: Índice
de Fragilidad
Qz:
Contenido de cuarzo.
Carb:
Contenido de carbonato.
Arcilla:
Cantidad de arcilla.
COT:
Porcentaje en peso de COT.
En este algoritmo la cantidad de arcilla es una variable muy
importante a tomar en cuenta, ya que, con esta es generado un desbalance de la
ecuación debido a que, si el material o la roca bajo tensión tiene una gran
región de comportamiento elástico, pero sólo una pequeña región de
comportamiento plástico, no absorbe mucha energía antes de fallar, por lo que
se considera frágil.
Rickman (2008) también propone otra forma de estimar el índice de
fragilidad combinando el módulo de Young y la relación de Poisson (Ecuación 6).
Este método propone que la relación de Poisson refleja la habilidad de la roca
a fallar bajo cierto esfuerzo y el módulo de Young está relacionado con la
habilidad de mantener la fractura abierta.
Para el cálculo del índice de fragilidad se debe obtener el módulo
de Young dinámico y la relación de Poisson a partir del registro sónico dipolar
(Ecuación 7), según Mullen (2007).
Ecuación 6
Ecuación 7
Donde:
Ed:
Modulo de Young dinámico.
ʋ: Relación de Poisson.
ρ: Densidad de bulk.
Δts: Tiempo de transito de corte
Δtc: Tiempo de tránsito compresional.
Para determinar el módulo de Young estático y la relación de
Poisson estática se puede hacer usando correlaciones locales o con mediciones
de laboratorio. Para usos prácticos se sabe que en lutitas, no existe
diferencia entre la relación de Poisson dinámica y estática (Mullen, 2007), y
el módulo de Young estático se puede obtener a partir de la Ecuaciones 8 y 9.
Ecuación 8
Ecuación 9
Donde:
Ed:
Modulo de Young dinámico.
Es:
Modulo de Young estático.
Debido a que las unidades del módulo de Young y la relación de
Poisson son muy diferentes entre sí, se le agregan constantes que son valores
límite para unificar los resultados (Ecuaciones 10 y 11).
Ecuación 10
Ecuación 11
Los valores unificados son sumados y promediados, siendo el valor
final un coeficiente de porcentaje (Ecuación 12).
Ecuación 12
En la Figura 4 se muestra la gráfica de la relación del módulo de
Young y la relación de Poisson para determinar el índice de fragilidad.
Fuente:
Rickman 2008.
Figura
4: Gráfico cruzado del módulo de Young y la relación de Poisson.
Al obtener el estudio del comportamiento frágil o dúctil de la formación se debe analizar y estimar el comportamiento de la fractura que se desea inducir, efectuando un modelo de fracturas adecuando con base a la información existente.
Intervalos
objetivos o Sweet Spots
Los intervalos de interés o Sweet Spots,
corresponden a un nombre que se otorga al lugar o áreas objetivos dentro de uno
o varios segmentos de la formación donde se puede generar la mejor producción
potencial. Los ingenieros toman en cuenta los aspectos geomecánicos,
petrofísicos y geoquímicos para determinar y representar dentro de cada pozo
perforado, las áreas prospectivas para la producción de hidrocarburos dentro
del yacimiento. Los Sweet Spots dentro de yacimientos no convencionales pueden
definirse por la riqueza o espesor de la roca generadora, por fracturas
naturales o factores geoquímicos que indiquen aspectos relevantes en el estudio
de la misma; utilizando datos geológicos para analizar núcleos extraídos de las
perforaciones realizadas, datos extraídos de registros eléctricos y datos
sísmicos (Galuccio, 2014).
Una formación con un índice de fragilidad igual o
mayor a 40% representa una formación
técnicamente fracturable hidráulicamente (12). Sin embargo,
para formación con menor valores de fragilidad pueden ser considerados como
sweet spots, pero el fluido utilizado a fracturar debe ser apropiado.
Las figuras a continuación muestran los valores
obtenidos con relación al índice de fragilidad en función a la mineralogía de
formaciones de Shale Gas a nivel mundial (Fernández et al., 2015), a pesar de
obtenerse este índice por el 20%, fue aceptable.
Figuras 5 y 6: Fragilidad en
función de la mineralogía en formaciones tanto en Usa como en Europa (Fernández
et al., 2015).
Para definir los sweet spots en el trabajo de
Fernández et al., (2015), se recolectaron los valores de COT de las principales
formaciones que por el índice de fragilidad mostraron valores por encima de
20%, y que mostraron por lo menos un 2% (%wt) del COT calculado, tal como se
muestra en la siguiente Tabla 1 (14).
Tabla 1. Intervalos de interés definidos bajo
parámetros de fragilidad y COT (Fernández et al., 2015).
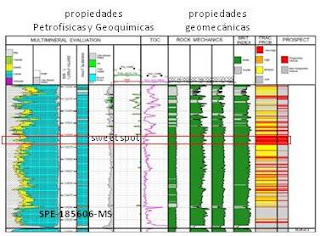
En la siguiente figura se muestra un set de
registros eléctricos ya evaluados donde después de integrar los resultados de
los parámetros geoquímicos como COT y geomecánicos como Módulo de Young,
relación de Poisson, la dirección de los 3 esfuerzos y el índice de fragilidad,
se determinan los intervalos prospectivos a proponer para la geonavegación de
los pozos:
Figura 7:
Shale evaluation results for La Luna Formation, Well PL-1402 SPE – 185606-MS (Lobo
et al., 2017) (16).
Para
determinar los intervalos prospectivos de los yacimientos no convencionales
tipo shale gas, se establecen una serie de cut-offs basados en la experiencia
tenida en los múltiples “plays” de los Estados Unidos (Boyer et al., 2006.
Jarvie et al., 2007; Sone and Zoback, 2012), mostrados en la siguiente tabla 2 (14).
Tabla 2. Intervalos de interés definidos bajo
parámetros de fragilidad y COT (Fernández et al., 2015).
Es
así que podemos entonces hablar de las zonas de aterrizaje o “landing zones”
para ir en busca de una mejor productividad obtenida en la combinación de la
geonavegación y fracturamiento hidráulico.
De
acuerdo con Lazzari (2017), el punto de aterrizaje o zonas de aterrizaje (landing zones) pertenece a las
coordenadas objetivos del proyecto de perforación el cual ha sido establecido
por medio de estudios previos en el área geológica del yacimiento, el punto de
aterrizaje indica la profundidad a la cual el pozo se completará y drenará el área
donde se encuentran presentes los hidrocarburos, los intervalos de interés o Sweet Spots proporcionan una visión más
clara al definir el objetivo, ya que han sido analizados a través de datos
geológicos que permiten lograr una mayor precisión en el punto de aterrizaje,
dado que es indispensable cumplir con las necesidades del proyecto respecto de
la recuperación final.
En
los yacimientos no convencionales es importante conocer la profundidad a la
cual se desea perforar, debido a que al considerar un proceso de fracturamiento
hidráulico en la zona productora, el pozo suele estar asociado a un tipo de
perforación horizontal, con la finalidad de poder obtener la mayor área de
drenaje permitida por el yacimiento y con ello, generar una producción de
hidrocarburo rentable (Galuccio, 2014).
En
la próxima figura, se muestra compuesta de un registro de pozo con sus
intervalos prospectivos maximizados en lo que se ha seleccionado para realizar
los landing zones, de base a tope y luego de forma lateral con los espaciamientos
debidamente evaluados para no interferir cada pozo, así como también las etapas
de fractura.
Figura 8: Ejemplo gráfico de selección
de los landing zones (IAPG, 2020).
Espero
que les haya sido de su agrado estos conceptos y primeras lecturas sobre el
abordaje de los YNC tipo Shale Gas en cuanto a su evaluación. Les dejamos las
referencias para su comprensión más en detalle.
Ing.
Eliana Alvarado G.
Referencias
Bibliográficas:
1.-
Cook John (2008). Articulo Técnico, “Oilfield Review 28, No 1” presentado por
la empresa Schlumberger, Oil Shale.
2.-
Ramírez, Ángel (2021). Generación y evaluación de un modelo geomecánico
analítico para la simulación del fracturamiento hidráulico de pozos. Trabajo
Especial de Grado a ser presentado ante la ilustre Universidad Central de
Venezuela, Facultad de Ingeniería, Escuela de Ingeniería de Petróleo.
3.-
Almeida y Cornielis, 2010. Correlaciones entre las clasificaciones
geomecánicas. [Trabajo especial de grado, Universidad Nacional de Colombia].
4.-
Guacuto, J. y Azocar, Y. (2017). Caracterización Geomecánica del Yacimiento
Eoceno Frac B2-X-68, para el Diseño de Fracturas en la Unidad de Producción
Lagunillas Lago, Lago Norte, Estado Zulia. [Trabajo especial de grado,
Universidad Central de Venezuela]. Repositorio institucional Saber UCV. http://saber.ucv.ve/handle/123456789/18047.
5.-
Gutiérrez, M., Lewi, R.W. (1970). “The role of geomechanics in reservoir simulation”.
SPE/ISRM Paper 47392.Trondheim, Norway, vol. 2, pp. 439–448.
6.-
Faría, A., Crux., J., Pilloud, A., & Canache, M. 2000. Biostratigraphic
and Lithostratigraphic Study of the La Luna Formation and its Lateral
Equivalents in Western Venezuela. SEPM Research Conference Paleogeography and
Hydrocarbon Potential of the La Luna Formation and Related Cretaceous Anoxic
Systems.7.-Vilas, B., Gonzales, A., Hernández, M., Quintero, F., Ricaurte, P.,
Rojas, I., Toribio, E., Vargas, A. “Estado del arte lutitas gasíferas”. PDVSA INTEVEP. No. de documento: SEA-0226, 2011.
8.-
Morley JE, Vellas B, Van Kan GA. (2013). “Frailty consensus: a call to action”. J Am Med Dir Assoc; 14:392-7.
9.- Hetényi M. (1966).
Handbook of experimental stress analysis. New
York. John Wiley & Sons, Quinta edición.
10.-
Ramsay S. (1967). Influencia de la fragilidad con respecto al campo de esfuerzo
de las rocas. J Am Soc. 66(3): 473-479.
11.-
Gutiérrez A. (2015). “Estudio de los yacimientos no convencionales de lutitas
petrolíferas y su potencial de explotación en la Formación La Luna en
Venezuela”. [Trabajo especial de grado, Universidad Central de Venezuela].
12.- Rickman, R., Mullen,
M., Petre, E., Grieser, B., and D. Kundert, (2008). A practical use of shale
petrophysics for stimulation desing optimization: All shale plays are not
clones of the Barnett shale, SPE 115258, Denver, Estados Unidos.
13.- Mullen, M., R.
Roundtree, and B. Barree (2007). A composite determination of rock properties
for stimulation desing (what to do when you don’t have a sonic log), SPE
108139, Denver, Estados Unidos.
14.-
Fernández, L. Quintero, Y., Calderón, Z. (2015). Análisis de la Fragilidad para
identificar sweet spots en formaciones de Shale Gas. Revista Fuentes. El
Reventón Energético. Vol. 13 N°2. Jul-Dic – pp-103/110.
15.-
Galuccio
M., 2014. Articulo técnico “Walking rigs, Vaca Muerta” YPF.